Introduction to the Law of Large Numbers
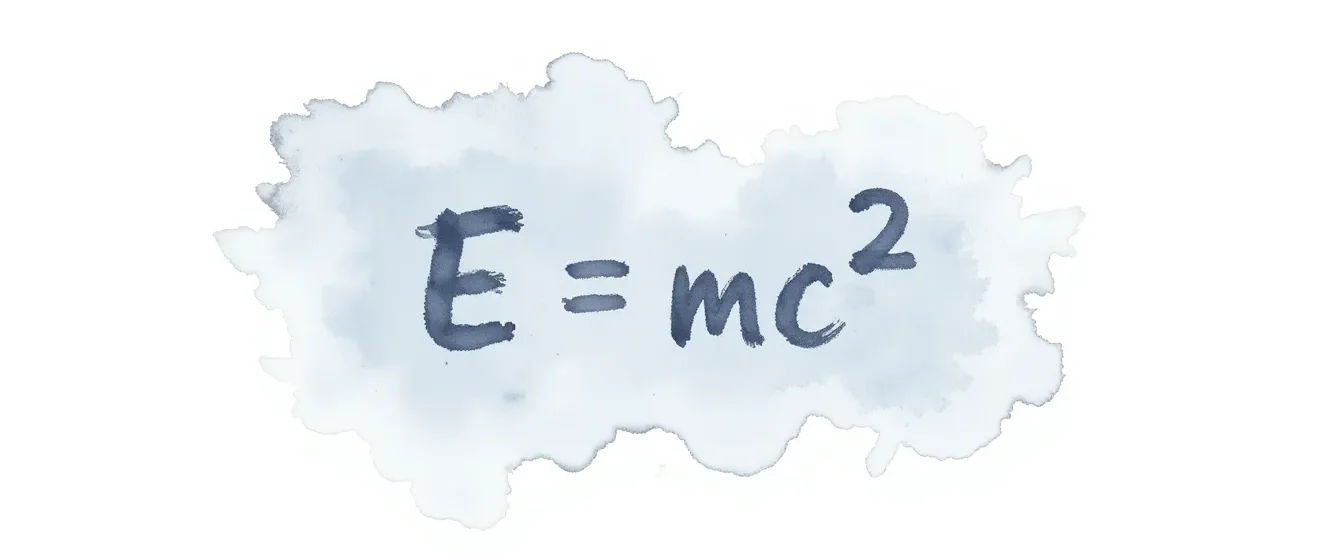
Definition and Significance
The law of large numbers serves as the mathematical foundation that supports modern risk management approaches. This core statistical principle indicates that as sample sizes increase, actual outcomes tend to approach what we’d expect based on theoretical probability. Insurance professionals rely on this concept to develop robust underwriting approaches, set fair premiums, and maintain stable portfolios across various areas, including health insurance and life insurance.
This mathematical principle works through two primary forms: the weak version and the strong version. The weak form illustrates how sample averages converge toward population averages as sample sizes increase, while the strong form provides mathematical proof that this convergence occurs. Both ideas play essential roles in insurance work, where large groups of policyholders help insurers forecast claim patterns with impressive precision.
Random elements in insurance—like claim sizes, loss patterns, and how long policies last—become much more predictable when combined across big portfolios. This predictability allows insurance carriers to price their products competitively while setting aside sufficient funds for claim payments. The real-world application extends beyond theory, as actual historical data confirms the mathematical principles underlying insurance production.
Historical Context in Insurance
The application of statistical principles in insurance dates back to the 1600s, when mathematicians began formalizing the concept of probability. Early ship insurers at Lloyd’s of London naturally used these ideas by spreading risks across many ships and trips. This historical base set up how modern insurance works today, where number-crunching drives wise business choices.
Moving from gut-feeling risk assessment to complex mathematical models shows how the insurance business has evolved. Today’s insurers utilize advanced statistical methods, including the central limit theorem and the Monte Carlo method, to gain a deeper understanding of how risks are distributed. These advances have transformed insurance from a risky bet into a precise financial tool backed by solid mathematics.
Current applications of these statistical principles extend far beyond traditional actuarial mathematics. Insurance companies now use probability distribution functions, including the Bernoulli distribution, the exponential distribution, and the Pareto distribution, to model tricky risk situations. This mathematical expertise enables better pricing and enhanced risk selection, ultimately improving the industry’s ability to provide financial protection against various insurable risks.
The Role of the Law of Large Numbers in Insurance Risk Management

How the Law Enables Insurers to Evaluate Risks
Insurance companies rely on statistical principles to convert uncertain individual results into predictable group outcomes when assessing risks. When insurers examine random variables across large portfolios, they identify patterns that would be impossible to discern in smaller groups. This ability proves especially useful when dealing with rare but costly events that require extensive data to study properly.
The process begins with random sampling from the target group, where insurers collect information on claim patterns, severity spreads, and policyholder characteristics. Through statistical inference, risk managers can estimate the true population average for different risk factors. As the sample size increases, confidence intervals become narrower, providing greater certainty in risk assessments and enhancing the accuracy of their models in predicting outcomes.
Choosing risks becomes much more effective with these statistical principles. Underwriters can identify risk factors that consistently correlate with more claims or larger losses. This knowledge creates better risk sorting systems that improve how portfolios perform. The weak law ensures that patterns observed in large data sets reveal genuine relationships rather than random fluctuations, enabling a more accurate assessment of idiosyncratic and financial risks.
Modern risk evaluation uses advanced statistical methods, including hypothesis testing and stochastic process modeling. These approaches enable insurers to verify their risk models against real-world experience data. When the sample mean consistently matches the expected value across multiple time periods, insurers feel more confident about their risk assessment methods. The coefficient of variation and standard deviation help measure the stability and reliability of these estimates.
The Impact on Premium Setting
The premium calculation demonstrates the most direct application of statistical principles in insurance work. These principles enable insurers to set rates that accurately reflect expected losses while maintaining the profit margins necessary for long-term success. Without sufficiently large sample sizes, premium calculations would depend solely on theoretical probability, creating significant exposure to biased selection and pricing errors.
The mathematical principle indicates that observed loss patterns will converge toward their true underlying probabilities as the insured population increases. This movement lets actuaries create rate structures based on real evidence rather than guesswork. Insurance premiums become more accurate and competitive when backed by lots of historical data supporting the law of large numbers.
Rate-making processes benefit from understanding different probability patterns that control insurance losses. The normal distribution often applies to total claim amounts. In contrast, individual claim frequencies may follow a Bernoulli distribution or binomial distribution pattern. Recognizing these patterns enables more accurate premium calculations that account for all possible outcomes, including disaster scenarios.
Statistical analysis of whether premiums are adequate relies heavily on these statistical principles. Actuaries watch actual versus expected results across large books of business, using the sample average to judge pricing accuracy. When actual results differ significantly from expectations, statistical principles provide guidance on whether the changes reflect real shifts in risk patterns or temporary fluctuations. This process helps maintain proper solvency levels and ensures that insurance carriers can survive in the long term.
Understanding the Loss Ratio in Insurance

What is the Loss Ratio?
The loss ratio indicates the percentage of collected premiums that are paid out as claims, serving as a key measure of insurance performance. This number directly reflects the accuracy of underwriting and pricing decisions, making it central to risk management approaches. Loss ratios under 100% show profitable underwriting, while ratios over 100% suggest losses that need attention.
Finding loss ratios means comparing losses that happened to premiums earned over specific time periods. This comparison determines whether premium levels adequately compensate for the risks taken on. Insurance professionals utilize loss ratio trends to identify emerging risks, assess underwriting performance, and adjust pricing strategies accordingly.
Loss ratio analysis becomes more useful when applied to large portfolios, where statistical principles help mitigate random fluctuations. Small books of business may have big loss ratio swings because of individual large claims, while larger portfolios show more steady patterns that reflect underlying risk traits. This steadiness matters especially for lines such as fire insurance and casualty insurance, where individual losses can be huge.
How the Law of Large Numbers Affects Loss Ratios
Statistical applications greatly stabilize loss ratio performance across large portfolios. As policy numbers increase, actual loss ratios move toward their expected values, reducing the impact of random swings. This stabilizing effect helps insurance companies that want predictable financial performance and operational stability.
Random variables affecting loss ratios include claims frequency, loss frequency, and timing patterns. When combined across thousands of policies, these variables tend toward their expected values, making loss ratios more predictable and manageable. The weak law provides mathematical backing for this stabilizing effect, which helps maintain consistent loss costs over time.
Portfolio size directly affects loss ratio stability. Companies writing big volumes in specific business lines have more predictable loss ratios than those with smaller portfolios. This relationship explains why many insurers try to reach critical mass in their chosen markets—statistical principles reward scale with better predictability and returns to scale in risk management efficiency.
The law of truly large numbers warns that very unusual events become almost certain when sample sizes are big enough. Insurance professionals must account for this when analyzing loss ratios, recognizing that rare but severe events will inevitably occur across large portfolios. This understanding is especially important for specialized risk pools, such as the nuclear pool, where uncommon but high-impact events are a primary concern.
Case Studies: Real-World Applications
Successful Implementation of the Law of Large Numbers
A regional property insurer’s change shows the practical benefits of applying statistical principles. Initially, with a small portfolio of 10,000 policies, the company experienced volatile loss ratios, ranging from 45% to 180% annually. Management chose to expand systematically, focusing on reaching critical mass in their target markets to improve risk diversification and statistical benefits.
Over the course of five years, the insurer grew to 100,000 policies while maintaining strict underwriting standards. The larger portfolio showed remarkable stability in loss ratio, with yearly changes narrowing to a 15-percentage-point range. This stability enabled more competitive pricing and improved financial planning accuracy, demonstrating the risk reduction benefits of a larger insurance collective.
The company’s success stemmed from understanding that the expected value of their loss ratio would become more apparent with larger sample sizes. They invest in data collection and statistical analysis capabilities to track their progress toward achieving statistical benefits. The finite variance in their loss experience became apparent as the portfolio size increased, enabling better risk assessment and pricing.
Geographic spreading made the statistical benefits bigger for this insurer. By spreading risks across multiple states and weather patterns, they reduced connections among claims and got more stable overall results. This approach demonstrates how spreading risks across areas can enhance the numerical scale in applying statistical principles, particularly important for managing exposure to catastrophic losses.
Lessons Learned from Ineffective Strategies
A commercial lines insurer’s mistakes give valuable lessons about the limits and proper use of statistical concepts. The company attempted to achieve scale through rapid expansion, acquiring small blocks of businesses without conducting thorough research on their risk profiles or loss history.
The buying approach failed to recognize that statistical principles require similarly distributed risks for best results. Each bought block had different underwriting standards, coverage forms, and risk profiles, creating a mixed portfolio that didn’t benefit from statistical stabilization. Loss ratios remained volatile despite an increase in policies, highlighting the importance of consistent risk evaluation across the portfolio.
Management made their mistake worse by assuming that any increase in sample size would automatically improve the results. They ignored selection bias in their purchases, buying mainly troubled books of business from competitors wanting to leave problem markets. Statistical principles cannot overcome systematic underwriting problems or bad selection in risk pools.
Improving required a return to basic risk management principles. The insurer implemented consistent underwriting methods across all operations, eliminated incompatible business segments, and rebuilt its portfolio with similar risk characteristics. They also enhanced their individual risk rating processes to more accurately account for the unique characteristics of commercial insureds. Only then did they begin to experience the stabilizing effects of statistical principles and the related improvements in operational stability.
Conclusion
Summary of Key Points
Statistical applications in insurance provide the mathematical base for practical risk management approaches across the insurance industry. These principles enable insurers to transform individual uncertainties into predictable group outcomes through careful portfolio building and management. Understanding both the weak form and its practical limitations helps insurance professionals optimize their risk management approaches and maintain proper solvency levels.
Successful use requires attention to portfolio makeup, ensuring that similarly distributed risks contribute to statistical stability. The sample mean is most effective in approximating the population mean when the underlying risks share similar features and follow consistent underwriting standards. Random sampling and statistical inference support this process by providing mathematical evidence for observed patterns, thereby improving the overall predictive accuracy of insurance models.
Premium setting and loss ratio management benefit a lot from statistical principles, but only when used correctly. Insurance professionals must maintain adequate sample sizes while avoiding the trap of assuming that all claim experiences will automatically stabilize with scale. The probability theory behind these applications requires careful attention to distributional features and potential sources of bias, especially when dealing with complex aggregate loss distributions.
Future Trends in Insurance Risk Management

New technologies and data analytics abilities are expanding the uses of statistical principles in insurance. Machine learning systems can process vast amounts of information to identify risk patterns that would be impossible to detect through traditional methods. These tools enable more sophisticated random experiments and statistical modeling approaches, potentially altering how insurers assess and price risks.
Connecting real-time data streams enables continuous monitoring of how statistical convergence patterns evolve. Insurance companies can now track whether their actual experience aligns with theoretical expectations on an ongoing basis, rather than waiting for yearly reviews. This ability enables more responsive risk management approaches and faster corrective actions when needed, thereby enhancing overall operational stability.
Rule changes are also shaping how insurers apply statistical principles to risk management. Requirements for better capital modeling and stress testing rely heavily on understanding probability distributions and their behavior under extreme conditions. The characteristic functions of various loss distributions become more critical as regulatory frameworks get more sophisticated, pushing insurers to improve their statistical approaches constantly.
Climate change and changing risk landscapes present new challenges for applying traditional statistical methods. Insurance professionals must adapt their understanding of probability measures and repeated trials to account for non-stationary risk environments. Statistical principles remain valid, but their application requires constant improvement as underlying risk patterns change. This ongoing adaptation helps maintain the industry’s ability to provide effective financial protection against an ever-changing array of risks.
As the insurance industry continues to evolve, the fundamental principles of statistical analysis will remain central to risk management approaches. However, their application will become more sophisticated, using new data sources, advanced analytical methods, and a deeper understanding of complex risk interactions. By leveraging these developments, insurers can enhance their risk assessment capabilities, refine pricing accuracy, and ultimately deliver more effective and efficient financial protection to policyholders across all lines of business.
Frequently Asked Questions
The law of large numbers allows insurers to more accurately predict expected losses across many policyholders, enabling them to set fair and stable premiums.
By pooling a large number of similar risks, insurers can use the law of large numbers to predict the frequency and severity of claims with greater accuracy.
Risk diversification occurs when insurers spread exposure across many policyholders, so individual unpredictable losses balance out and overall risk becomes more predictable.
Reinsurance expands the pool of risks across multiple insurers, enhancing the stabilizing effect of the law of large numbers and reducing volatility from large or catastrophic losses.
Actuaries rely on the law of large numbers when analyzing historical data to forecast future losses, set reserves, and develop accurate pricing models for insurance products.

